Gas Discharge Flow Calculator for Choked and Subsonic Gas Flow Conditions

When is this calculator suitable?

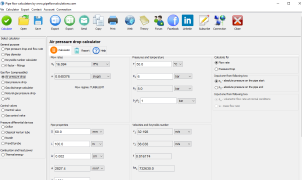
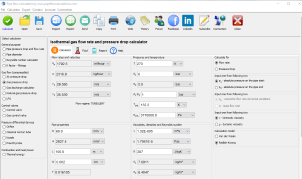
The Gas discharge flow calculator is a specialized tool designed to compute the flow rate of gases exiting pipelines or reservoirs, considering factors such as pressure differences, pipe diameters, and the presence of valves and fittings.

It supports calculations for various two- and three-atomic gases, including air, nitrogen, and carbon dioxide, under steady flow conditions with constant pressures.

The calculator employs the Darcy formula, modified for gas flow, and utilizes the Colebrook-White equation to determine friction factors. It also assesses whether the flow is choked and provides relevant calculations for such scenarios. Users can input parameters like resistance coefficients for valves and fittings, as well as pipeline surface roughness, to obtain accurate results.

You can use the calculator for flow in pipelines that include valves and fittings. You can calculate the maximum flow rate when you know pressure difference and pipe diameter, or you can calculate pipe diameter when you know flow rate and pressure drop.

The calculator is applicable for all two and three atomic gases, like air, nitrogen, carbon dioxide and other gases. The calculator is suitable for steady flow with constant pressures at one point of streamline.

What are the calculator restrictions?

The calculator is suitable for ideal gases, as the calculator uses the equation of state for ideal gas during calculation. The calculator is not applicable for non-steady, pulsating flow.

How is the calculation executed?

Based on the known pressure difference (head loss) between one point of flow stream at the start of a pipe or in front of a valve, to the outside point (like atmosphere), or after a valve with known inside pipe diameter, mass flow rate, and volume discharge flow rate is calculated. The calculator uses a modified Darcy formula for flow rate calculation.

$w=\mathrm{1.111\times }{\mathrm{10}}^{-6}{\mathrm{Yd}}^2\sqrt{\frac{\mathrm{\Delta p\rho }}{K}}$

where is:

w - offtake mass flow rate [kg/s]
Y - expansion factor [ - ]
d - internal pipe diameter [mm]
Δp - pressure drop [Pa]
ρ - density [kg/m3]
K - resistance coefficient [ - ]

The calculator is calculating a friction coefficient using the Colebrook-White formula:

$\frac{1}{\sqrt{f}}=\mathrm{-2.0}\log (\frac{k_{\mathrm{r}}}{\mathrm{3.7065D}}+\frac{\mathrm{2.5226}}{\mathrm{Re}\sqrt{f}})$

where is:

f - friction factor [ - ]
k - pipe roughness [mm]
D - internal pipe diameter [mm]
Re - Reynolds number [ - ]

The gas discharge calculator presents Reynolds number and expansion factor as calculation results.

The calculator is checking if a flow is choked or not and presents choked flow status. For choked flow conditions, the calculator is calculating the flow rate for that condition.

What else has to be known to perform the gas discharge calculation?

You should enter resistance factor K for valves and fittings if they exist in the pipeline as well as pipeline surface roughness.

When is this calculator not relevant?

The calculator is not relevant for liquids.