
Flow coefficients and pressure losses in valves, fittings, and orifices
Resistance coefficient K, flow coefficients Cv, Kv, Cg, Kg, and discharge through Venturi and nozzle
Read on this page
More on fluid dynamics
Resistance Coefficient (K) – Head Loss in Valves and Fittings, Equivalent Pipe Length (L/D)
Pressure drop or head loss is proportional to the velocity in valves or fittings. For the most engineering practices it can be assumed that pressure drop or head loss due to flow of fluids in turbulent range through valves and fittings is proportional to square of velocity.
To avoid expensive testing of every valves and every fittings that are installed on pipeline, the experimental data are used. For that purpose resistance coefficient K, equivalent length L/D and flow coefficient Cv, Kv are used. These values are available from different sources like tables and diagrams from different authors and from valves manufacturers as well.
Kinetic energy, which is represented as head due to velocity is generated from static head and increase or decrease in velocity directly is proportional with static head loss or gain. "Velocity head" is:

where is: hL - head loss; v - velocity; gn - acceleration of gravity;
The number of velocity heads lost due to resistance of valves and fittings is:

where is: hL - head loss; K - resistance coefficient; v - velocity; gn - acceleration of gravity;
The head loss due to resistance in valves and fittings are always associated with the diameter on which velocity occurs.
The resistance coefficient K is considered to be constant for any defined valves or fittings in all flow conditions, as the head loss due to friction is minor compared to the head loss due to change in direction of flow, obstructions and sudden or gradual changes in cross section and shape of flow.
Head loss due to friction in straight pipe is expressed by the Darcy equation:

where is: hL - head loss; f - friction factor; L - length; D - internal diameter; v - velocity; gn - acceleration of gravity;
It follows that:

where is: K - resistance coefficient; f - friction factor; L - length; D - internal diameter;
Try the Resistance Coefficient Calculator
Calculate resistance coefficient K and equivalent length l/d with this calculator. This calculator is applicable for liquids and gases and provides resistance coefficient calculation for many different valves and standard fittings.
The ratio L/D is equivalent length in pipe diameters of straight pipe that will cause the same pressure drop or head loss as the valves or fittings under the same flow conditions. As the resistance coefficient is K is constant the equivalent length L/D will vary inversely with the change in friction factor for different flow conditions.
For geometrically similar valves and fittings, the resistance coefficient would be constant. Actually there are always smaller or bigger geometrical non similarity in valves and fittings of different nominal size, so the resistance coefficient is not constant. The resistance coefficient K for a given type of valves or fittings, tends to vary with size as does friction factor for straight clean commercial steel pipe at the same flow conditions.
Some resistances in piping like sudden or gradual contractions and enlargements, as well as pipe entrances or exists are geometrically similar. Therefore the resistance coefficient or equivalent length L/D is for these items independent of size.
The values for resistance coefficient or equivalent length L/D are always associated with internal pipe diameter where the resistance is occurring.
If the resistance coefficient or equivalent length L/D should be used for different internal pipe diameter than the diameter for which existing values can be found following relationship can be used:

where is: K - resistance coefficient; D - internal diameter;
where subscript "a" defines K and d with the reference to internal pipe diameter, and subscript "b" defines K and d with the reference to the internal diameter for which values of K can be found in tables or diagrams.
This equation can also be used if the piping system has more than one size of valves and fittings to express the resistance coefficient or equivalent length L/D in terms of one size.
Resistance Coefficient for Sudden and Gradual Contractions or Enlargements (K Values)
Using momentum, continuity and Bernoulli equation the resistance due to sudden enlargements may be expressed as:

and the resistance factor due to sudden contraction as:

where is: K1 - resistance coefficient; d1 - internal diameter (smaller); d2 - internal diameter (larger);
Using β as diameter ratio, both equation can be expressed as:

where is: K1 - resistance coefficient; β - diameter ratio d1/d2;
In order to express the resistance coefficient in terms of larger pipe diameter, following relation should be used:

where is: K1 - resistance coefficient based on smaller internal diameter; K2 - resistance coefficient based on larger internal diameter; β - diameter ratio d1/d2;
If the enlargement is not sudden but gradual, or if angle of gradual enlargement is different from 180O, Gibson coefficient Ce can be used for different angle of divergence as follows:


In other words, if angle of divergence is bigger than 45O, the resistance coefficient is equal to one for sudden enlargement.
For gradual contraction the resistance coefficient on the same basis based on Crane test data, contraction coefficient Cc can be used for different angles of convergence, as follows:


Using above expressions for enlargement and contraction coefficient, resistance coefficient can be calculated as:
For gradual enlargement:


where is: Ce - coefficient of enlargement; K1 - resistance coefficient based on smaller internal diameter; β - diameter ratio d1/d2; θ - enlargement angle;
For gradual contraction:


where is:
Cc - coefficient of contraction; K1 - resistance coefficient based on smaller internal diameter; β - diameter ratio d1/d2; θ - enlargement angle;
For resistance coefficient based on the large pipe diameter expression:

should be used, with above equations.
where is: K1 - resistance coefficient based on smaller internal diameter; K2 - resistance coefficient based on larger internal diameter; β - diameter ratio d1/d2;
Equations for gradual enlargement and contraction can be used for resistance coefficient calculation for reduced bore straight-through valves like ball valves and gate valves. The total resistance coefficient for this type of ball and gate valves is the summation of resistance coefficient for gradual contraction and gradual enlargement.
You can calculate resistance coefficient using resistance coefficient K and equivalent length l/d calculator.
Flow Coefficient (Cv, Kv) – Pressure Drop and Control Valve Flow Rate Calculation
Selecting the correct valve size for a given application requires knowledge of process conditions that the valve will actually see in service. In the industry of control valves it is practice to use flow coefficient and flow characteristics.
In the UK and in the USA coefficient Cv is used and it is defined as flow rate of water in gpm at 60OF that creates pressure drop of 1 psi across the valve. Basic equation for valve sizing for liquid service is:

where is: Cv - flow coefficient [gpm]; q - flow rate [gpm]; Δ p - pressure drop [psi]; S - specific gravity (relative density) [ - ];
Try the Control Valve Calculator
Calculate flow coefficient Cv or Kv of control valve. This calculator is applicable for calculation of maximum flow capacity of control valve and pressure difference. Calculate pressure difference for known flow coefficient Cv or Kv and flow capacity.
To aid in establishing uniform measurement of liquid flow coefficients Cv, standardized testing facility by Fluid Control Institute (FCI) are used by manufacturers. The effect of viscosity of fluids other than water should be considered when selecting the valve, as increased viscosity of fluid is reducing the valve capacity.
Another coefficient Kv is used in some countries, particularly in Europe and is defined as flow rate of water in m3/h that creates pressure drop of 1kg/cm2 across the valve (1 kg/cm2 is equal to 0.980665 bar).
Control valve sizing is based on the calculation of flow coefficient for given pressure drop and flow rate. Liquid flow capacity of a valve in metric units can be converted to Cv as:

where is: Cv - flow coefficient [gpm]; qm - flow rate [l/m]; ρ - density [kg/m3]; Δ p - pressure drop [bar];
Also, liquid flow capacity of a valve can be converted to Kv as:

where is: Kv - flow characteristic [m3/h]; qh - flow rate [m3/h]; S - specific gravity (relative density) [ - ]; Δ p - pressure drop [bar];
For additional reference, see the Flow coefficient (Cv/Kv) article on Wikipedia , which explains how the valve’s geometry and pressure drop define its performance.
Flashing and Cavitation in Valves – Vapor Pressure at Vena Contracta
Flashing or cavitation inside a valve can have a significant influence on valve capacity. Flashing and cavitation can reduce the flow through valve in many liquid services. Also, damage can be made to the valve as well as to the piping system. The effect is represented by the change from liquid to vapor state of fluid, resulting in the velocity increase downstream from the valve.
As liquid passes through the restriction area inside the valve flow stream is contracted. The smallest cross section area of stream is just downstream of the actual physical restriction at a point called vena contracta. At that point the velocity is at its maximum and pressure at the minimum.
As the fluid exits the valve, away from vena contracta, velocity decrease and pressure increase, so the critical point for flashing and cavitation is at the point where the pressure is smallest which is in vena contracta. If pressure at vena contracta drops bellows the vapor pressure of the fluid, due to increased velocity at this point, bubbles will form in the flow stream.
If pressure downstream of the vena contracta increase above the vapor pressure, bubbles will collapse or implode producing cavitation. Cavitation releases energy and produces a noise. If cavitation occurs close to solid surfaces, the energy released gradually wears the material leaving the rough surface. Cavitation can also damage the downstream pipeline, if at that place the pressure rises above the vapor pressure and bubbles collapse.
Choked Flow in Valves – Pressure Drop Limits and Cavitation Effects
Formation of bubbles in the valve resulting of flashing and cavitation effect reduces the flow rate through valve and limits the capacity. This is called chocked flow. Limiting pressure drop in valve is determined by experiment for each valve. Limiting pressure drop for chocked flow in valve can also be calculated using:

where is: Δ pallow - maximum allowable pressure drop for chocked flow[psi]; Km - valve recovery coefficient from manufacturer literature [ - ]; p1 - valve inlet absolute pressure [psia]; pv - vapor absolute pressure of the liquid at inlet temperature [psia]; rc - critical pressure ratio 0,70 - 0,95;
In high recovery valve, cavitation can occur on pressure drop below that produces chocked flow. Therefore cavitation index is used to determine the chocked flow pressure drop at which cavitation damage will begin in high recovery valve:

where is: Kc - cavitation index from manufacturer literature [ - ]; p1 - valve inlet absolute pressure [psia]; pv - vapor absolute pressure of the liquid at inlet temperature [psia]; pc - pressure drop that creates cavitation in high recovery valves [psi];
This equation can be used anytime outlet pressure is greater than the vapor pressure of the liquid.
Flow Through Orifices, Nozzles, and Venturi Tubes – Discharge Coefficients and Pressure Ratios
The rate of flow of any fluid through an orifice or nozzle, may be calculated using following equation:

where is: q - flow rate; Cd - coefficient of discharge; A - cross section area; β - diameter ratio d1/d2; gn - acceleration of gravity; hL - head loss;
Instead of coefficient of discharge Cd, more convenient is the use of flow coefficient C which is represented by:

where is: C - flow coefficient; Cd - coefficient of discharge; β - diameter ratio d1/d2;
Flow rate through nozzles and orifices are than calculated as:

where is: q - flow rate; C - flow coefficient; A - cross section area; Δ p - pressure drop; ρ - density; gn - acceleration of gravity; hL - head loss;
The values of hL and Δ p are measured differential static head or pressure before and after the nozzle or orifice. Values for coefficient of discharge or flow coefficient (C or Cd) can be calculated based on applicable standards like ISO 5167 or similar ASME standards.
Coefficient of discharge for orifice flow can be calculated using Reader-Harris/Gallagher (1998) equation (ISO 5167):

where is: β - diameter ratio d1/d2; ReD - Reynolds number based on bigger diameter; d1 - internal diameter (smaller); d2 - internal diameter (larger);
Try the Orifice Flow Calculator
Calculate orifice plate diameter, discharge and expansion factor. This calculator is applicable for for liquids and perfect gases. Calculate flow rate from measured pressure drop according to ISO 5167.
L1 and L2 are functions on tap type and it is:
L1=L2=0 - for corner taps
L1=1; L2=0.47 - for D and D/2 taps
L1=L2=0.0254/d1 - for d1[m] for 1" taps
Example #7
Task: Calculate flow rate of air through the orifice plate. Orifice internal diameter is 100mm, and tube where orifice is inserted, internal diameter is 200mm. Pressure in front of the orifice is 104000 Pa, and pressure after the orifice is 100000 Pa absolute. Pressures are measured on the corner taps. Temperature of air is 15 C.
Solution: Flow rate is: 1374.5 m3/h
Example #8
Task: Calculate flow rate of water flowing through orifice plate with external diameter of 120 mm and internal diameter of 80 mm. Measured pressures in front and after the orifice is 11000 mm H2O and 10000 mm H2O. Pressure is measured on 1 inch taps.
Solution: Flow rate is: 54.674 m3/h
Example #9
Task: Calculate flow rate of water through the orifice with external diameter of 200 mm, internal diameter of 160 mm. Measured pressure drop in front of the orifice is 10729 mm H2O and measured pressure drop is 400 mm H2O. Pressures are measured at corner taps
Solution: Flow rate is: 155.94 m3/h
Coefficient of discharge for Venturi tubes can be obtained based on the type of Venturi tube. There are three types of Venturi tubes and each type has different range of diameters and Reynolds number for which coefficient of discharge is defined as follows:
Venturi tubes with "as cast" convergent section Cd=0.984;
Range for which coefficient of discharge is defined:
100 mm < D < 800 mm
0.3 < β < 0.75
2x10e5 < ReD < 2x10e6
Venturi tubes with a machined convergent section Cd=0.995;
Range for which coefficient of discharge is defined:
50 mm < D < 250 mm
0.4 < β < 0.75
2x10e5 < ReD < 2x10e6
Venturi tubes with a rough-welded sheet-iron convergent section Cd=0.985;
Range for which coefficient of discharge is defined:
200 mm < D < 1200 mm
0.4 < β < 0.7
2x10e5 < ReD < 2x10e6
Try the Venturi Flow Calculator
Calculate Venturi tube diameters based on the created pressure drop by Venturi effect. This calculator is applicable for for liquids and perfect gases. Calculate Venturi effect from measured pressure drop according to ISO 5167.
Coefficient of discharge for nozzles is calculated based on the type of nozzle in question. For nozzles according to ISA 1932 coefficient of discharge can be calculated using following formula:

Coefficient of discharge for long radius nozzles is calculated using:

and for Venturi type nozzles:

where is:
β - diameter ratio d1/d2; ReD - Reynolds number based on bigger diameter;
Try the Nozzle Flow Calculator
Calculate Nozzle diameters based on the created pressure drop by Venturi effect. This calculator is applicable for for liquids and perfect gases. Calculate nozzle size and velocities from measured pressure drop according to ISO 5167.
For the flow of compressible fluids through nozzles and orifices, the same equation can be used, but the net expansion factor Y must be included. The flow can be calculated as follows:

where is: Y - expansion factor; C - flow coefficient; A - cross section area; Δ p - pressure drop; ρ - density;
The expansion factor Y depends on the specific heat ratio χ , the diameter ratio β and the ratio of downstream and upstream absolute pressures.
Expansion factor Y for Venturi tubes and nozzles can be calculated as follows (ISO 5167):
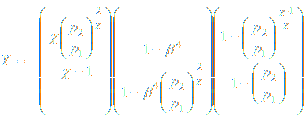
This equation is applicable for the same range of diameter and Reynolds number as for coefficient of discharge Cd indicated above. Formula is applicable only for pressure ratio p2/p1 > 0.75.
For compressible flow through orifices expansion factor is (ISO 5167):

where is: Y - expansion factor; χ - specific heat ratio; β - diameter ratio d1/d2; p1 - inlet pressure; p2 - pressure in Venturi throat or after the orifice or nozzle;
This equation can be used for gas flow though the orifice and discharging to the atmosphere. For that purpose the pressure difference equals to the upstream gauge pressure. This applies only if absolute atmospheric pressure divided by absolute upstream pressure is bigger than critical pressure ratio for sonic flow conditions.
When the smoothly convergent nozzle is used compressible fluid can reach the speed of sound at minimum cross section or throat, if upstream pressure is high enough.
When the velocity of compressible fluid reaches the speed of sound, maximum flow has been reached, and increase of upstream pressure or decrease of downstream pressure will not increase the flow any more.
For short tubes where relation L/D is not bigger than 2.5 the flow of discharge to the atmosphere can be calculated using above equations, with flow coefficient C somewhere between the values for orifice and nozzle.
If the entrance to the short tube is well rounded then the flow coefficient C for nozzles can be used and if the pipe entrance is square shaped and sharp then flow coefficient C for orifice is more appropriate.
Liquid and Gas Discharge Through Valves and Fittings – Application of Resistance Coefficient (K)
For discharge of liquids through valves, fittings and pipes Darcy formula can be expressed as:

where is:
q - discharge flow rate [l/min]; d - internal pipe diameter [mm]; hL - head loss [m]; K - resistance coefficient [ - ];
This equation can be used for offtake calculation from pipes, fittings and valves when resistance coefficient K, static head difference hL and internal pipe diameter d is known. The resistance coefficient is the sum of all resistances in the piping system.
For offtake of compressible flow of fluid from a pipe to a larger area or larger cross section like in the case of offtake to the atmosphere, a modified Darcy formula can be used:

where is:
w - offtake mass flow rate [kg/s]; Y - expansion factor [ - ]; d - internal pipe diameter [mm]; Δ p - pressure drop [Pa]; ρ - density [kg/m3]; K - resistance coefficient [ - ];
Try the Gas Discharge Calculator
Calculate actual or maximum gas outflow from pipes, valves and reservoirs for given pressure difference and opening size. This calculator applies adiabatic compressible gas flow equations for perfect gases, appropriate for sudden pressure changes like during the outflow from small openings.
Gas Pressure Regulator Capacity – Flow Coefficients (Cg, Kg) and Critical Flow Rate Equations
For gas pressure regulators that are operating in the range of inlet pressure up to 100 bar following equations for sub-critical and critical flow behavior are used (EN 334):
Sub-critical flow:
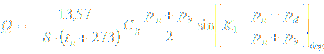
Critical flow:
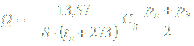
where is:
Q - gas flow rate [m3/h]; S - gas relative density (for air=1) [ - ]; tu - gas upstream temperature [OC]; Cg - gas flow coefficient [ - ]; pu - gas upstream pressure [bar]; pd - gas downstream pressure [bar]; pb - ambient atmospheric pressure [bar]; K1 - valve body shape factor [ - ];
Try the Gas Control Valve Calculator
Calculate flow coefficient Cg or Kg or maximum capacity of control valve for upstream and downstream pressure. This calculator calculates pressure drop that control valve is creating for known flow rate and flow coefficient Cg or Kg.
Simplified calculation can be used if K1 < 130 and (pu-pd) > 0,1 (pu+pb):
Sub-critical flow rate where (pu-pd) < 0,5 (pu+pb):
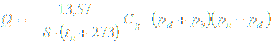
Sub-critical flow rate where (pu-pd) > 0,5 (pu+pb):
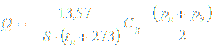
Above equation can be expressed with flow coefficient Kg included as:
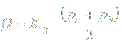
With above equations when flow coefficient Cg or Kg from gas pressure regulator manufacturer is known, regulator capacity can be calculated for given pressures upstream and downstream from gas regulator.
It can be concluded that if pressure of gas before and after the regulator are higher, capacity of regulator will also be higher for the same type and dimension of regulator.
When flow rate through regulator is critical, pressure downstream of the regulator doesn't influence the regulator capacity.
It is important also to notice that for different type of gases that have different value of density, capacity of regulator will also change, and for gases with higher densities, flow rate will be smaller and volume capacity will drop.
All equations are for regulators with fully opened control element, as flow coefficient are measured for fully opened regulator. Capacities for different positions of control element in regulator are calculated related to the curve of appropriate regulator.
Natural Gas Control Valve Flow Rate – Pressure Ratios and Correction Factors
For control valves in natural gas industry it is common to use KG which is defined for under critical pressure ratio (pa/pe > 0.54) as:

For overcritical pressure ratio (pa/pe < 0.54):

where is:
KG - flow coefficient [m3/h] qn - flow rate at normal conditions (p = 101325 Pa, T = 273,15 K) [m3/h] pa - pressure after the control valve [bar] pe - pressure in front of the control valve [bar]
For other gases, correction factor should be used as:

where is correction factor:

where is:
qn NATURAL GAS - flow rate at normal conditions of natural gas [m3/h] qn GAS - flow rate at normal conditions of other gas [m3/h] f - correction factor [ - ]
Continue with Practical Calculations
Use these engineering tools to apply the formulas from this page to real cases:
- ➤ Orifice Flow Calculator — for orifice plate diameter, discharge and expansion factor.
- ➤ Venturi Tube Calculator — for Venturi tube diameters calculation from created pressure drop by Venturi effect.
- ➤ Nozzle Flow Calculator — for Nozzle diameters calculation from created pressure drop by Venturi effect.
- ➤ Control Valve Calculator — for calculation of flow coefficient Cv or Kv of control valve
- ➤ Gas Control Valve Calculator — for calculation of flow coefficient Cg or Kg or maximum capacity of control valve for upstream and downstream pressure
- ➤ Resistance Coefficient Calculator — for calculation of resistance coefficient K and equivalent length l/d
